使用WPF学习计算机图形学——一个古老的绘制器一文中介绍了德国画家丢勒绘画时使用的一种装置,线的一端固定到墙面上,另外一端放置在待绘制物体表面的某个点,记录线穿过木框的位置,并在画纸关闭时标记到画纸上,通过不断变动线末端物体上的点最终就可以绘制出一幅准确的物体画像,丢勒使用的其实就是一种透视投影装置,使用这种方式可以绘制出真实立体感的图形。

在计算机图形学中,投影变换目的就是把场景世界中的3D物体转换为2D平面图形的过程,转换后降了一维,相对于前面的绘图装置,线末端固定点的可以认为是观察者的视点或者摄像机的位置。依据这个目的,我们的目标本质上就是已知物体表面的点坐标(x,y,z)计算出投影的某个固定面的2D坐标(x',y',1),可以根据三角形的比例关系轻松的计算出x'=x/z,y'=y/z。
假定物体投射到z=1的平面上,因为投影是把3D降维转换为2D,所以z的坐标是固定不变的

就这么简单?然而,在计算机图形学中透视投影变换是一种比较复杂的变换,实际的计算远远比刚才的计算复杂得多,那么是什么增加了计算的复杂度哪?
首先,实际的图形学投影变换需要考虑摄像机的视域体,下图中从相机出发的金字塔形的锥体区域为视域体,其中只有近裁切面和远裁切面之间范围内的物体才会进行绘制,之外的物体需要进行忽略或裁切;另外,由于绘制图形的屏幕有各种各样的规格尺寸,为了简化计算大部分的图形库都会首先变换到规范化立方体内(各坐标轴坐标范围为-1~1)进行处理,因为这样就无需考虑屏幕的尺寸,最终输出图形时还会再通过反变换输出到屏幕坐标系中。

这两种因素导致了实际的投影变换比较复杂,接下来我们来一步步推导出透视投影变换矩阵。
正交投影首先,从简单的正交投影矩阵推导开始,正交投影矩阵也叫平行投影,投影的方向和坐标轴要么平行要么垂直。正交投影可以有下面两个步骤组合来完成:
1.把下图左侧由前后、上下、左右裁切面组成的长方体盒型视域体的中心点平移到右侧规范化立方体的坐标原点,这一步为平移变换。
2.通过缩放把长方体盒型视域体变换为规范化立方体,这一步为缩放变换,且为非均匀缩放。
这里需要特别说明的是,由长方体非均匀缩放后变换为立方体肯定会导致绘制图形的拉伸导致图形的比例失调,但是不会扭曲,因为进行的是线性变换,之所以变换到规范化立方体纯粹是为了计算的简化,最后输出到屏幕时还会通过反变换的方法重新恢复原有的比例。
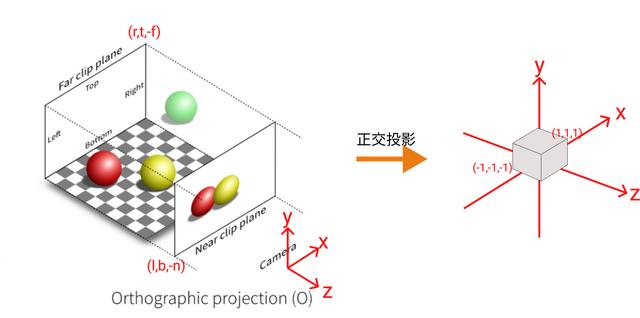
设(Xe,Ye,Ze)为变换前的长方体区域内的任意坐标点,Xe的取值范围为(l,b),Ye的取值范围为(b,t),Ze的取值范围为(-n,-f),(Xn,Yn,Zn)为该点变换到规范化立方体后的坐标点,则根据线性变换的特性(直线经线性变换后仍然是直线)以及三角形相似性原理可以得出下面的公式。
由于摄像头视线朝向z轴的反方向,z轴方向的坐标一般为负值,离摄像头越远值越小

求解可以得出下面的结果

将上面的公式改写为矩阵的形式如下,其中Mortho即为正交投影矩阵:

正交投影无论离摄像头的距离有多远,投影出来的大小都是一样的,这个跟真实观察的场景是不一样的,就像两条平行的铁轨在远处会交会到一个点,也就是常说的近大远小,要达到这种效果需要用到透视投影。
正交投影也有广泛的用途,如CAD的主视图、左视图、俯视图就采用正交投影
透视投影的视域体形状为如下图左侧所示四锥体区域,类似于正交投影,透视投影的四锥体中心点变换到规范化立方体的原点,四锥体区域经变换后成为规范化立方体。

可以把透视投影拆解成两个步骤,首先把远裁切面收缩到和近裁切面同样大小的面(由于采用线性变换,远近裁切面之间的区域也会相应地收缩,越远收缩程度越大,这样就形成了近大远小的效果),这样视域体就成了和正交投影一样的长方体区域;接下来,再进行一次正交投影就可以变换到规范化立方体区域了,见如下示意图。而正交投影矩阵已经推导出来了,现在只需要推导出第一步的收缩矩阵即可。

四锥体收缩为长方体的过程遵循以下规则:
1.近裁切面的所有点坐标保持不变;
2.远裁切面的所有点z坐标不变,都是-f;
3.远裁切面的中心点坐标保持不变,为(0,0,-f)。
设(Xe,Ye,Ze)为四锥体视域体中的任意点坐标,经过收缩变换后的坐标为(X',Y',Z'),收缩矩阵为Mpersp,其中近裁切面的x轴坐标范围为(l,r),y轴坐标范围为(b,t),z轴坐标为-n。根据三角形的相似性原理,则可以得出:


这里需要利用齐次坐标的一个性质,所谓齐次坐标就是使用n 1维来表示n维坐标,具体为何要这样使用请自行查询资料学习,这里需要用到齐次坐标的一个性质,如果(x,y,z,1)表示投影到w=1平面的点坐标,那么(nx,ny,nz,n)坐标投影到w=1平面的是同一个点(nx/n,nz/n,nz/n,n/n)=(x,y,z,1),这就是齐次坐标的尺度不变性。
有了上面的特性,上面的公式得到的结果同时乘以Ze可得:

Mpersp为4x4矩阵,根据上面的公式我们能得出矩阵的第一、二、四行的值,如下

矩阵的第三行还是未知数,根据远裁切面中心点的坐标(0,0,-f)保持不变、近裁切面坐标保持不变这两个规则可以得出


最终得出收缩矩阵为

最后,收缩矩阵Mpersp再进行正交投影就得到了透视投影矩阵,透视投影矩阵Mper为: